Einleitung
- In EidP ging es bisher vor allem um: Syntax, Datentypen, Kontrollstrukturen, Funktionen, Zeiger
- Jetzt der nächste Schritt: Vom „Code schreiben“ zum „Problem lösen“
- Dazu brauchen wir zwei Bausteine:
- Datenstrukturen: Wie speichern/organisieren wir Daten?
- Algorithmen: Wie arbeiten wir effizient mit diesen Daten?
- Fokus heute: typische Datenstrukturen kennenlernen und praktisch einsetzen
- Nicht „alles selbst implementieren“, sondern: passende Werkzeuge auswählen (STL) und richtig benutzen
- Merksatz: Anforderungen → passende Operationen → passende Datenstruktur
Problem
Wir bauen (konzeptionell) ein kleines Tool: z.B. digitaler Notizzettel
Es kommen „Ereignisse“/Aufgaben rein, werden verarbeitet und teilweise rückgängig gemacht
Anforderungen (Operationen):
- Neue Aufgaben in Ankunftsreihenfolge abarbeiten
- „Letzte Aktion“ rückgängig machen / ggf. wiederherstellen
- Elemente vorn/hinten hinzufügen/entfernen (z.B. Priorisierung)
- Daten einfügen/löschen, während wir gerade „mittendrin“ sind (z.B. Verlauf/Historie)
- Optional: Werte schnell finden (z.B. nach ID/Name)
- Frage, die wir beantworten wollen: Welche Datenstruktur unterstützt welche Operationen natürlich und effizient?
Stapel (Stack)
Klassisches Beispiel für lineare Datenstruktur: (Keller-)Stapel
Funktionsweise zur Genüge bekannt (→ Kapitel Zeiger)
→ Hier nicht noch mal Thema
- Stattdessen: Typische Operationen der zugrundeliegenden Datenstruktur
push: legt Element oben auf den Stapelpop: entfernt oberstes Element vom Stapeltop: gibt das oberste Element vom Stapel zurückempty: prüft, ob Stapel leer istsize: gibt Anzahl der Elemente zurück
- Arbeitsprinzip: Last In, First Out (LIFO)
Beispiel - Stapel
- Glücklicherweise müsst Ihr den Stack nicht implementieren
- STL bietet bereits eine fertige Lösung:
std::stack
#include <stack>
#include <iostream>
using std::cout, std::endl;
int main() {
std::stack<int> int_stack;
int_stack.push(42);
int_stack.push(4711);
cout << "Top: " << int_stack.top() << endl; // Element wird *nicht* entfernt
int_stack.pop(); // Wegwerfen. Rückgabe 'void' -> Zugriff nur mit top()
cout << "New Top: " << int_stack.top() << endl;
}Warteschlange (Queue)
- Weitere, verbreitete Datenstruktur: Warteschlange (Queue)
- Typische Operationen
enqueue: fügt Element hinten andequeue: entfernt vorderstes Elementfront: gibt vorderstes Element zurückback: gibt letztes Element zurückempty: prüft, ob Warteschlange leer istsize: gibt Anzahl der Elemente zurück
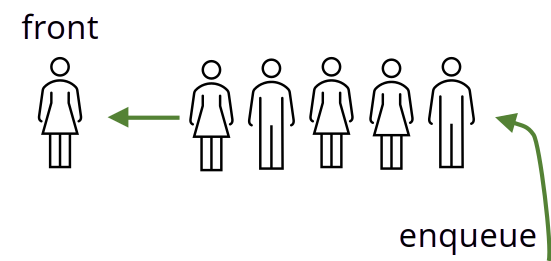
- Arbeitsprinzip: First In, First Out (FIFO)
Beispiel - Warteschlange
- Auch hier gibt es eine STL-Implementierung:
std::queue
#include <queue>
#include <iostream>
using std::cout, std::endl;
int main() {
std::queue<int> int_queue;
int_queue.push(42);
int_queue.push(4711);
int_queue.push(5);
int_queue.push(3);
cout << "Front: " << int_queue.front() << endl; // Analog zu Stack: Kein Entfernen
cout << "Back: " << int_queue.back() << endl; // Analog zu Stack: Kein Entfernen
int_queue.pop(); // Entfernen ohne Verwenden
cout << "New Front: " << int_queue.front() << endl;
}Warteschlange (Queue)
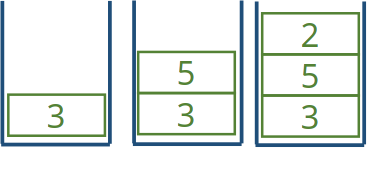
- Erweiterung der einfachen Warteschlange: Double-Ended Queue (Deque)
- Im Gegensatz zur einfachen Warteschlange ist hier auch das Hinzufügen am Anfang erlaubt:
push_front/push_backund analogpop_front/pop_back
#include <deque>
#include <iostream>
using std::cout, std::endl;
int main() {
std::deque<int> int_deque;
int_deque.push_front(42);
int_deque.push_back(4711);
int_deque.push_front(5);
int_deque.push_back(3);
cout << "Front: " << int_deque.front() << endl;
cout << "Back: " << int_deque.back() << endl;
int_deque.pop_back();
cout << "New Back: " << int_deque.back() << endl;
}Verkettete Listen (Linked Lists)
- Einfache Grundidee: Aneinanderreihung von Daten
Jedes Element kennt Inhalt
Jedes Element kennt Nachfolger
→ Kettenglieder bzw. Knoten(Nodes)
- Zwei Varianten
- Einfach verkettet: Nur Verweis auf den Nachfolger
- Doppelt verkettet: Verweis auf Nachfolger und Vorgänger
- Einfachste Umsetzung in C++: Mittels Zeigern
- Erstellen eines Startelements , dann sukzessives Hinzufügen
Verkettete Listen (Linked Lists)
- Einfach verkettete Listen sind unkompliziert, aber in der Praxis eher unhandlich
- Falls einmal der Vorgänger benötigt werden sollte, muss im schlechtesten Fall die gesamte Liste erneut vom Start aus traversiert werden
- Doppelt verkettete Listen sind hier deutlich handlicher:
- Bei Bedarf kann einfach ein Element an Ort und Stelle eingefügt werden
- Daraus ergeben sich einige interessante Anwendungsbereiche:
- Beispiele: Verlaufshistorie im Browser, Textbearbeitung (Strg-Z, Strg-Y)
- Bei Änderungen kann einfach ab einem beliebigen Punkt alles Nachfolgende entfernt und neues Element angehängt werden
Beispiel - Verkettete Listen
- C++ bietet bereits doppel-verkettete Liste:
std::list - Ähnliche Signatur wie Deque
- Wesentlicher Unterschied
insert: fügt Element an Position X einerase: entfernt vorderstes Element
#include <list>
#include <iostream>
using std::cout, std::endl;
int main() {
std::list<int> l;
l.push_front(5);
l.push_front(10);
l.push_back(20);
auto pos = l.end();
l.insert(pos, 42);
cout << "Back: " << l.back() << endl;
l.pop_back();
cout << "Back: " << l.back() << endl;
}Bäume
- Häufig verwendete Datenstruktur
- Zahlreiche Anwendungen
Suchen von Elementen
→ B-Trees (Datenbanken), Rot-Schwarz-Bäume
Aufteilen von Raum
→ Binary Space Partitioning (z.B. in Videospielen)
Min-/Max-Heaps
→ Grundlage von Prioritätswarteschlangen
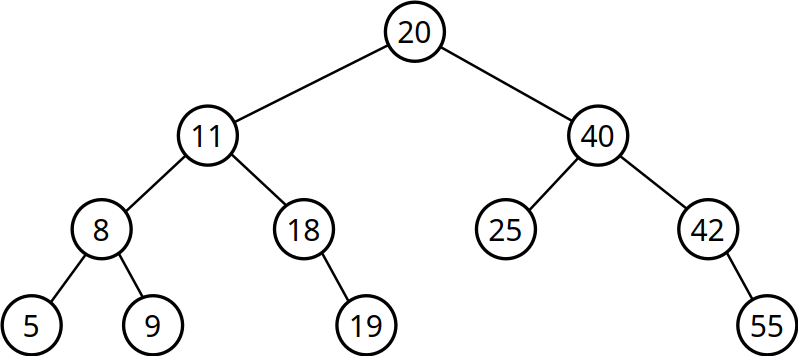
- Hier und heute: Binärbaum - einfachste Form eines Baums
Binärbäume
- Besteht aus Knoten (Nodes)
- Startknoten → Wurzel des Baums (Root)
- Endknoten → Blätter des Baums (Leafs)
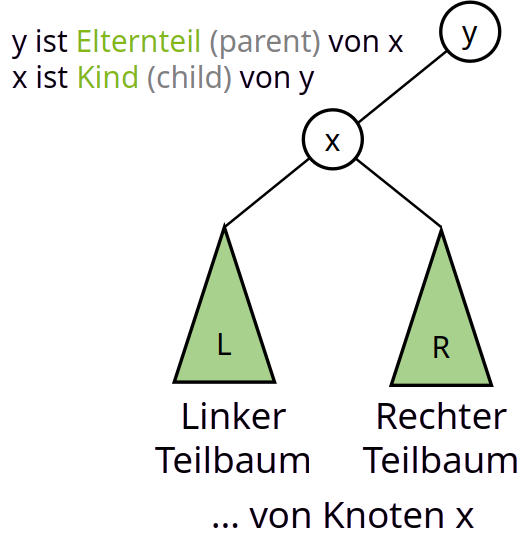
- Vorgängerknoten → Elternteil (Parent)
- Nachfolgeknoten → Kind (Child)
- Jedem Knoten wird ein Wert zugewiesen
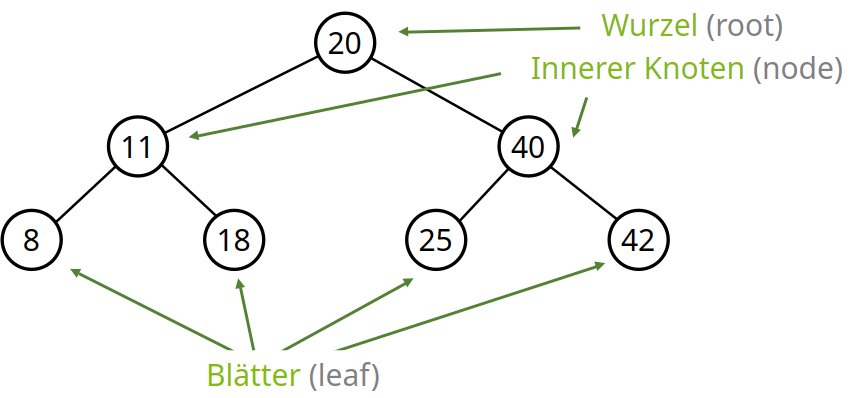
- Jeder Knoten hat höchstens zwei Kindknoten → binär
- Suchbaumeigenschaft
- Linkes Kind ist kleiner
- Rechtes Kinds ist größer
Eigenschaften von Binärbäumen
Wurzel hat keine Vorfahren
Blätter hingegen haben keine Kinder
→ Linkes und rechtes Kind
Darf aber auch nur einen/keinen Kindknoten besitzen
Pfad: Folge von zusammenhängenden Eltern-Kind-Knoten
Definition erfolgt rekursiv
Höhe eines Baumes
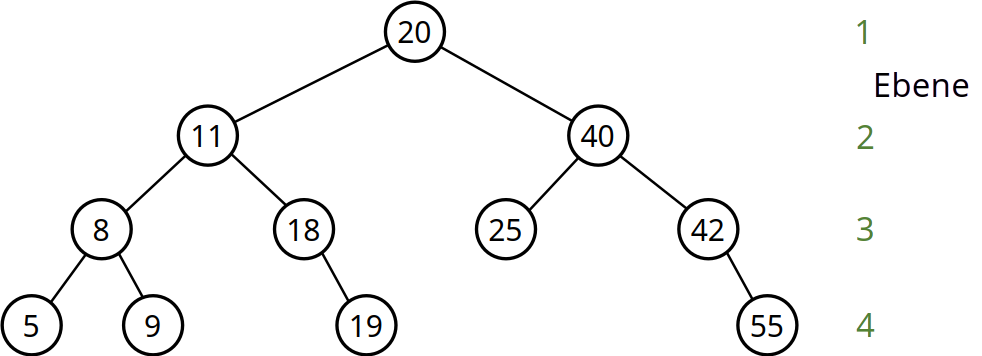
- Höhe eines Baums ist die Anzahl der Knoten auf dem längsten Pfad im gesamten Baum
- Betrachung von Wurzel zu Blatt
- Höhe eines leeren Baums:
0, da keine Knoten vorhanden - Beispiel: \(20,40,42,55\)

Größe eines Baumes
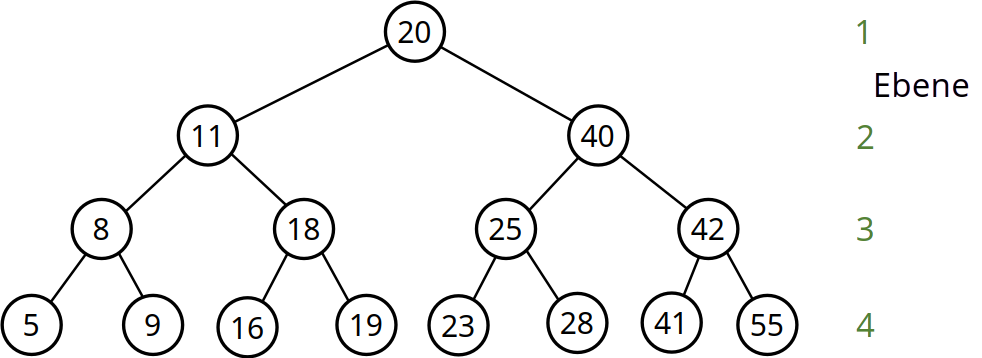
- Ebene \(k\): Knoten mit Abstand \(k-1\) zur Wurzel
- Auf Ebene \(k\) können jeweils zwischen \(1\) und \(2^{k-1}\) Elemente liegen
- Max. Anzahl Elemente bei Höhe \(h\): \(\sum_{k=1}^{h} 2^{k-1} = 2^h -1\)
Eigenschaften von Binärbäumen
- vollständiger Baum der Höhe \(h\) besitzt \(2^h-1\) Knoten
- Sei \(n = 2^h-1\): Dann braucht man höchstens nur \(\lceil log_2(n)\rceil\) Schritte, um ein Element zu suchen!
- Beispiel: \(n=100 \Rightarrow \lceil log_2(100)\rceil = \lceil 6.64\rceil = 7\)
- Degenerierter Baum
- Aus Baum wird eine Liste
- Bei \(n\) Knoten wären dann wieder \(n\) Vergleiche notwendig (\(O(n)\) statt \(O(log{}\text{ }n\)))
- Ein extremes Gegenbeispiel (Worst Case) → entspricht Liste

Vorteile von Binärsuchbäumen
- Erlaubt schnelle Suche
- Ablauf
- Falls gleich → Ende der Suche, alle sind glücklich
- Ansonsten
- Gesuchtes Element ist kleiner → nach Links
- Gesuchtes Element ist größer → nach rechts

- Großartige Eigenschaft: Bei Auswahl des nächsten Teilbaums fallen alle anderen Teilbäume weg
- Bei (balancierten) Binärbäumen halbiert sich der verbleibende Suchraum im besten Fall automatisch
Stolpersteine
- Nur ein Baum mit gefüllten Ebenen benötigt wenig Schritte für die Traversierung
- Ziel: gleichmäßig befüllen oder nachträglich balancieren
- Nur bei balancierten Bäumen liegt die Suchzeit bei \(O(log{}\text{ }n)\)
- Zur Balancierung gibt es eine Reihe von verschiedenen Algorithmen
- Klassisches Beispiel: Rot-Schwarz-Bäume
- Abwechselnde Einfärbung der Ebenen mit rot und schwarz
- Anschließend Balancieren basierend auf der Farbe
Durchlaufstrategien
- Zwei Arten der Traversierung
- Breitensuche (Breadth-First Search)
- Tiefensuche (Depth-First Search)
- Preorder: Zuerst ganz nach links, dann schrittweise nach rechts
- Inorder: Reihenfolge der Knotenwerte (aufsteigend)
- Postorder: Erst alle Kinder, dann den aktuellen Knoten
- Unterschiedliche Suchmuster können bei der Ausgabe/Darstellung des Baums hilfreich sein
Beispiel - Durchlaufstrategien

- Für Tiefensuche (DFS): Rekursion verwenden
- Breitensuche (BFS) verwendet hingegen eine Warteschlange (hier nicht dargelegt)
Beispiel - Durchlaufstrategien

- Je nach Strategie andere Ausgabe:
- Preorder: \(20, 11, 8, 5, 9, 18, 19, 40, 25, 42, 55\)
- Inorder: \(5, 8, 9, 11, 18, 19, 20, 25, 40, 42, 55\)
- Postorder: \(5, 9, 8, 19, 18, 11, 25, 55, 42, 40, 20\)
Beispiel - Durchlaufstrategien

- Praktische Anwendung:
- Erstellen einer Kopie (Preorder)
- Ausgabe des Baums (Inorder)
- Löschen des Baums (Postorder)
Hashing
- Hashing ist ebenso wie Binärbäume weit verbreitet
- Ziel: Erstellen einer eindeutigen Kennung, um Daten identifizieren zu können
- Abstraktes Beispiel: Postleitzahl schränkt Zustellungsort ein
- 44227 → Dortmund (Eichlinghofen)
- Abbildung von Daten erfolgt mit Hashfunktionen
Mathematische Abbildung, erzeugt aus Daten einen sogenannten Hashwert
→ eindeutiger Indentifizierer
- Nützliche Eigenschaften von Hashwerten
- In der Regel deutlich kleiner als die Daten
- Rückschluss auf zugrundeliegende Daten im Allgemeinen nicht möglich
Hashing
- Großer Zahlenraum der Hashwerte notwendig
- Erlaubt eindeutige Zuordnung zwischen Hashwert und Daten
- Ansonsten: Mehrere Daten haben den gleichen Hashwert (→ Hashkollision)
- Beispiel: \(h(x) = x \mod 10\) → schlechte Hashfunktion
- Sehr einfach, aber maximal 10 mögliche Hashwerte (0 - 9) → viele Kollisionen
- Zahlenraum der möglichen Werte der Hashfunktion sollte deutlich größer sein als die Zahl der tatsächlichen Hashwerte
- Eigenschaften einer guten Hashfunktion
- Vermeidet Kollisionen oder macht sie zumindest sehr unwahrscheinlich
- Voraussetzung: Möglichst „zufällig“, damit der Hashwert möglichst gleichverteilt im Zahlenraum liegt
- Einfach zu berechnen!
- Vermeidet Kollisionen oder macht sie zumindest sehr unwahrscheinlich
Hashing
- Es existieren zahlreiche Hashfunktionen mit unterschiedlichen Einsatzgebieten
- Einige Anwendungen
Indexierung: unter anderem Datenbanken, Caches, Dictionaries
Kryptographie: z.B. Hashwert aus Passwort berechnen, Abspeichern des Hashes (
bcrypt)[Dateivergleich: Prüfen der Integrität von großen Dateien durch separaten Hashwert (
SHA1,MD5)Bloom-Filter: unter anderem Spam-Filter, schnelles Nachschauen von Symbolen
→ Linker des GCC-Compilers bei dynamischen Bibliotheken
Blockchain: Bei Bitcoins wird fortwährend
SHA-256(kryptographische Hashfunktion) berechnet
Dictionary
- Dictionary (Wörterbuch) ist eine spezielle Datenstruktur
- Speichert Schlüssel zusammen mit Wert (Key-Value-Pairs)
- Drei Kernoperationen:
- Insert
- Delete
- Search
- Gute Umsetzung: Mittels Hashtabelle
Dictionary
Speichern für jeden Hash assoziierte Daten
Hashkollisionen: Erstellen einer Linked-List für diesen Hashwert
Gute Hashfunktion → wenig/keine Kollisionen
Unwahrscheinliche Kollision
→ i.d.R. wenige Schritte für Nachschlagen
→ konstante Zeit
Dictionaries sind gut für schnelles und zuverlässiges Nachschauen geeignet
Dictionary in Programmiersprachen
- Dictionaries existieren in zahlreichen Programmiersprachen
- Java:
HashMap<K,V> - C#:
Dictionary<K,V> - Python:
dict()bzw.{}(sehr starke Verwendung) - … und noch vielen weiteren mehr
- Java:
- C++: STL-Container namens
std::unordered_map - Achtung Verwechslungsgefahr: In C++ gibt es außerdem
std::mapstd::mapist allerdings mit Red-Black-Bäumen umgesetzt (→ keine Hashtabelle)
Beispiel - std::unordered_map
#include <iostream>
#include <string>
#include <unordered_map>
using std::cout, std::endl;
int main() {
std::unordered_map<int, std::string> int_str_dict = {
{1, "Eins"}, // Key und Value
{2, "Zwei"},
};
// Insert
int_str_dict.insert({42, "Zweiundvierzig"});
int_str_dict.insert({4711, "Siebenvierzigelf"});
cout << int_str_dict[42] << endl; // Lookup: Version Nr.1
// Fallstrick: operator[] erzeugt in C++ automatisch neues Element,
// falls es nicht vorhanden ist. Besser: Methode at()
try { // at() kann Exception werfen!
int_str_dict.erase(1); // Delete
cout << int_str_dict.at(1) << endl; // Lookup: Version Nr.2
} catch(std::out_of_range &err) {
cout << "Error: " << err.what() << endl;
}
}Dictionaries werden Euch noch oft begegnen. Es lohnt sich, sie zu kennen!
Exkurs: Graphen
- Weiteres großes Gebiet der Mathematik und Informatik: die Graphentheorie
- Ein Graph ist eine abstrakte Struktur, die verschiedene Objekte (Knoten) miteinander über Kanten verbindet
- Einfache Anwendungsbeispiele
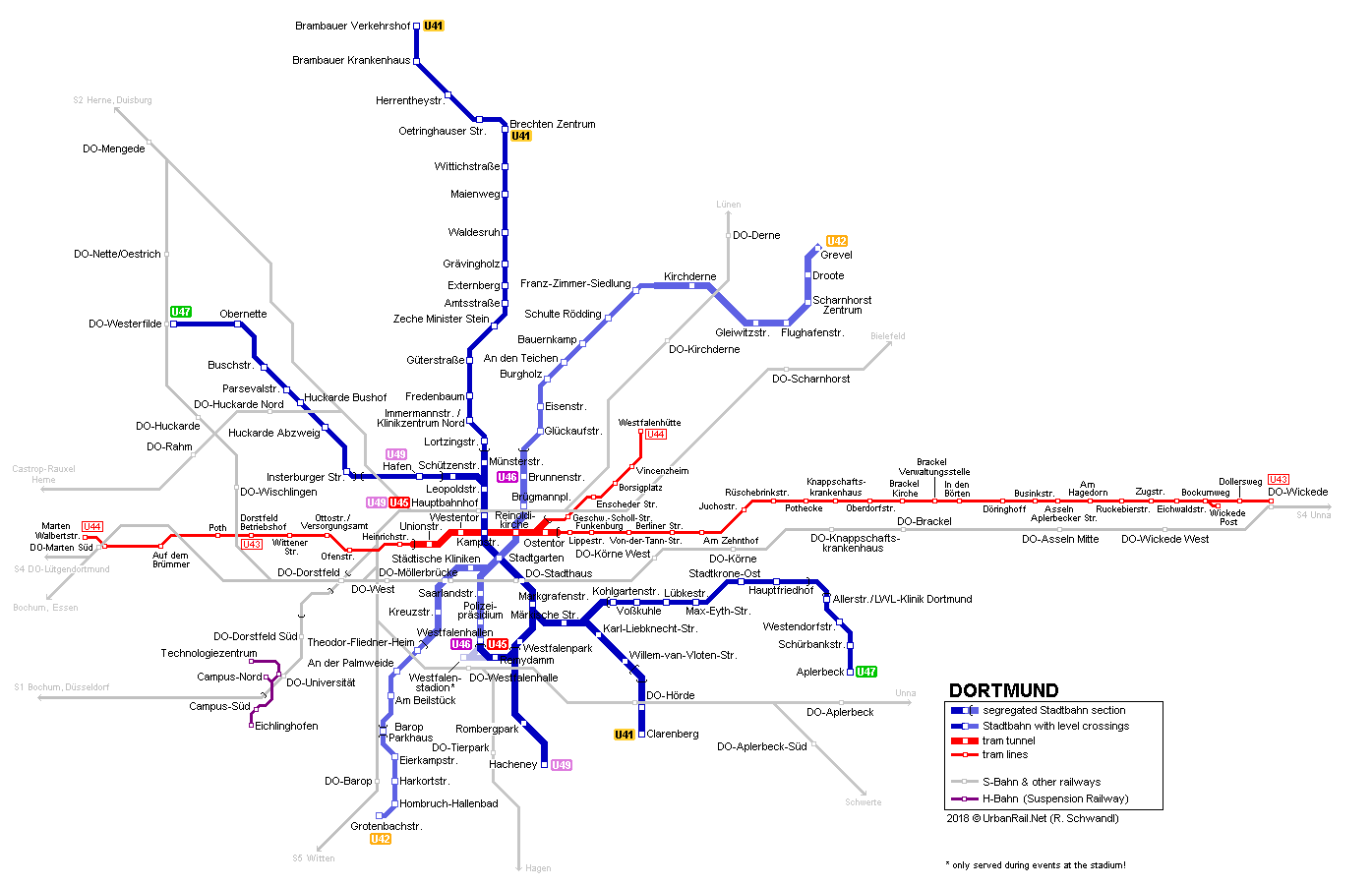
- Navigation → Straßenbahn und Verkehr
- Netzwerke → Computernetzwerke/Internet, aber auch Funkverbindungen (z.B. überlappendes Mobilfunknetz)
- Soziale Netzwerke → Abbildungen von Interaktionen und Gruppen (Social Media Bubbles)
- Layout-Fragen bei elektronischen Schaltungen
Übrigens: Ein Binärbaum ist auch nur ein spezieller Graph 😊
Beispiele für Graphen
- Einfaches Beispiel: Nord-Campus als Graph
- Kreuzungen sind Knoten, Straßen sind Kanten
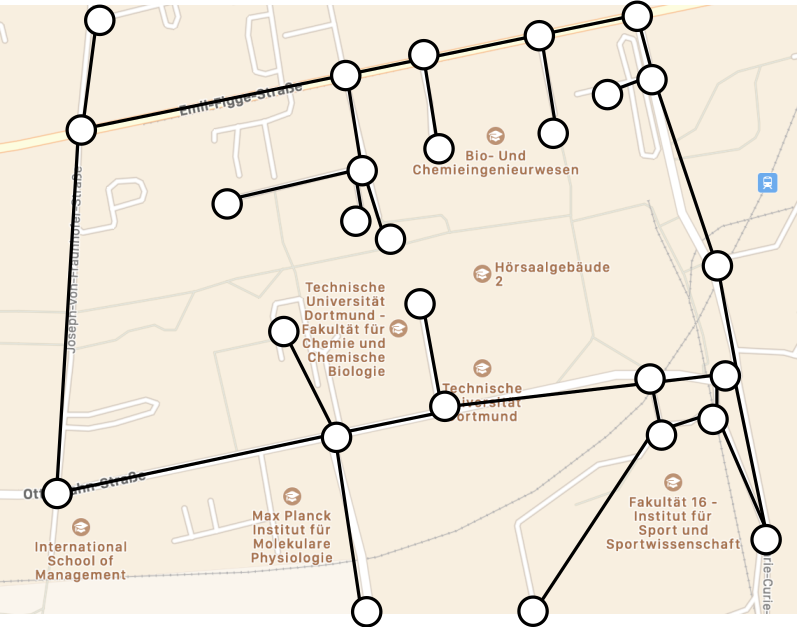
Beispiele für Graphen
- Graphen sind sehr vielseitig: Chemische Verbindungen als Graph darstellbar
- Beispiel: Koffein als Graph dargestellt
- Atome → Knoten, Bindungen → Kanten
Definition von Graphen
- Graph \(G = (V,E)\) besteht aus
- einer Menge \(V\) von Knoten (Vertex bzw. Plural Vertices) und
- einer Menge Kanten \(E\) (Edges) mit \(E \subseteq V \times V\) (→ „jedes E wird aus zwei V gebildet”)
- \(V = \{1,2,3,4,5\}\)
- \(E = \{(1,2),(1,5),(2,3),(2,5),(3,3),(3,4),(3,5),(4,5)\}\)
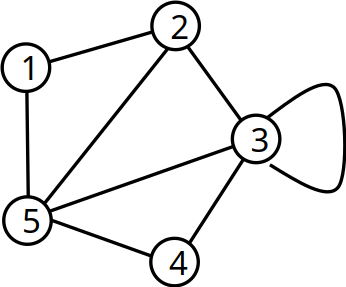
- Grad (degree) eines Knotens \(v \in V\) ist die Anzahl an adjazenten Knoten
- Mit anderen Worten: Alle zu \(v\) durch eine Kante verbundenen Knoten sind adjazent
- Beispiel: \(deg(5) = 4\) → „5 hat vier Nachbarn”
Speicherung von Graphen
- Abschließend: Exemplarische Speicherung von Graphen
- Zwei Möglichkeiten: Adjazenzliste oder Adjazenzmatrix
- In der Praxis: Adjazenzliste, weil Matrix \(O(n^2)\) Speicher und Zeit braucht
- Außerdem: Viele Graphen haben Lücken (sparse) → viele
0in Matrix
- Adjazenzmatrix: Setze in 2D-Array bei Kante
1, sonst0

- Adjazenzliste: Erstelle für jeden Knoten Liste mit Nachbarn
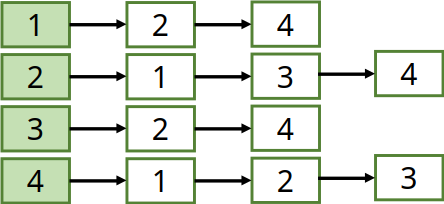
Weitere Algorithmen der STL
- STL besteht hauptsächlich aus von Containern, Algorithmen und Iteratoren
- Container: Die Wichtigsten wurden vorgestellt ✅
- Iteratoren: Bereits kurz vorgestellt ✅
- Algorithmen: Implementierung besonders häufig verwendeter Funktionen (noch nicht betrachtet)
- Zum Abschluss noch einige interessante Teile des Algorithmen-Teils
- Algorithmen arbeiten meist mit Iteratoren (oder wandeln Eingabe automatisch in einen Iterator um)
- Sind in Headern
<algorithm>,numericundmemoryzu finden (Link)- Unbedingt reinschauen! Sehr viele Funktionen, die einem das Leben erleichtern!
Beispiel - std::accumulate
std::accumulate: Addiert die Zahlenwerte in einem STL-Container automatisch
#include <iostream>
#include <vector>
#include <numeric>
using std::cout, std::endl;
int main() {
std::vector<int> vec = {1, 3, 5, 10};
// Parameter 3: 0 ist der Startwert der Summe
int result = std::accumulate(vec.begin(), vec.end(), 0);
cout << "Sum of vector: " << result << endl;
}Beispiel - std::count
- Zählt die Anzahl der Elemente, die einen vorgegebenen Werten haben
#include <iostream>
#include <vector>
#include <algorithm>
using std::cout, std::endl;
int main() {
std::vector<int> vec = {1,2,3, 3, 5, 10, 14, 17, 3, 18, 22, 42};
int count_3 = std::count(vec.begin(), vec.end(), 3);
cout << "Number of 3: " << count_3 << endl;
}Beispiel - std::sort
- Sortiert vorgegebene Elemente in aufsteigender Reihenfolge
- Absteigende Reihenfolge:
std::greater()und ggf. Operatoroperator<implementieren
- Absteigende Reihenfolge:
#include <iostream>
#include <vector>
#include <algorithm>
using std::cout, std::endl;
int main() {
std::vector<int> vec = {5, 2, 1, 10, 4, 42};
cout << "Original: \t";
for (const int& i: vec) {
cout << i << ", ";
}
std::sort(vec.begin(), vec.end());
cout << "\nSorted: \t";
for (const int& i: vec) {
cout << i << ", ";
}
// std::greater() (und std::less()) rufen Vergleichsoperator operator< auf
std::sort(vec.begin(), vec.end(), std::greater<int>()); // Default für int generieren
cout << "\nReverse: \t";
for (const int& i: vec) {
cout << i << ", ";
}
}Beispiel - std::transform
- Wendet eine Operation schrittweise auf jedes Element eines Containers an
#include <iostream>
#include <vector>
#include <algorithm>
using std::cout, std::endl;
template <typename T>
T double_val(T value) {
return value * 2;
}
int main() {
std::vector<int> vec = {5, 2, 1, 10, 4, 42};
cout << "Original: \t";
for (const int& i: vec) {
cout << i << ", ";
}
std::transform(vec.begin(), vec.end(), vec.begin(), double_val<int>);
cout << "\nTransformed: \t";
for (const int& i: vec) {
cout << i << ", ";
}
}Ausblick
Ein sehr kleiner Einblick in die Welt der Algorithmen und Datenstrukturen
Für ein gutes Programm ist auch ein Verständnis dieses Bereichs notwendig
Anders ausgedrückt: Gute Entwickler:innen müssen neben dem Programmieren auch verstehen, was entwickelt werden muss und wie dies effizient möglich ist
→ Mischung aus gutem Verständnis der Programmiersprache und der Algorithmen
Ausblick
Wir waren hiermit gestartet …
- Programmierung als Bindeglied
- zur echten Welt und
- praktische Umsetzung von theoretischen Problemen
- TODO Abschließende weise Worte
Ausblick: Wo geht die Reise weiter?
- Für diejenigen, die nach EidP noch weiter programmieren wollen
- Modul Datenstrukturen, Algorithmen und Programmierung 2 (DAP2)
- Pflichtmodul für Informatiker:innen, im Sommersemester
- Die Inhalte, die in diesem Kapitel angesprochen wurden, in detaillierter Form und noch einiges mehr!
- Viele Algorithmen und Datenstrukturen mit praktischer Umsetzung. Macht Spaß 😊
- Modul Betriebssysteme (BS)
- Pflichtmodul für Informatiker:innen, ebenfalls im Sommersemester
- Wichtige, weiterführende Konzepte: nebenläufige Programmierung, Speicher/Caches, …
- Sehr wichtig zum Verständnis des Embedded-Bereichs!
Abschlussarbeiten
Ihr schreibt bestimmt irgendwann einmal eine Abschlussarbeit 😀
Wenn Euch Hardware-nahe und/oder Betriebssystem-nahe Themen interessieren, denkt gerne an uns! 😀
Wir interessieren uns auch für Themen aus der E-Technik.
Meldet Euch dann gerne bei uns: https://sys.cs.tu-dortmund.de/
Tschüss!
🤞 Viel Erfolg 🤞
und vielen Dank für die Aufmerksamkeit! 🙏
Am Donnerstag gibt es eine Fragestunde!
Bitte bereitet Fragen zum Stoff vor.